PINE LIBRARY
BenfordsLaw
Updated
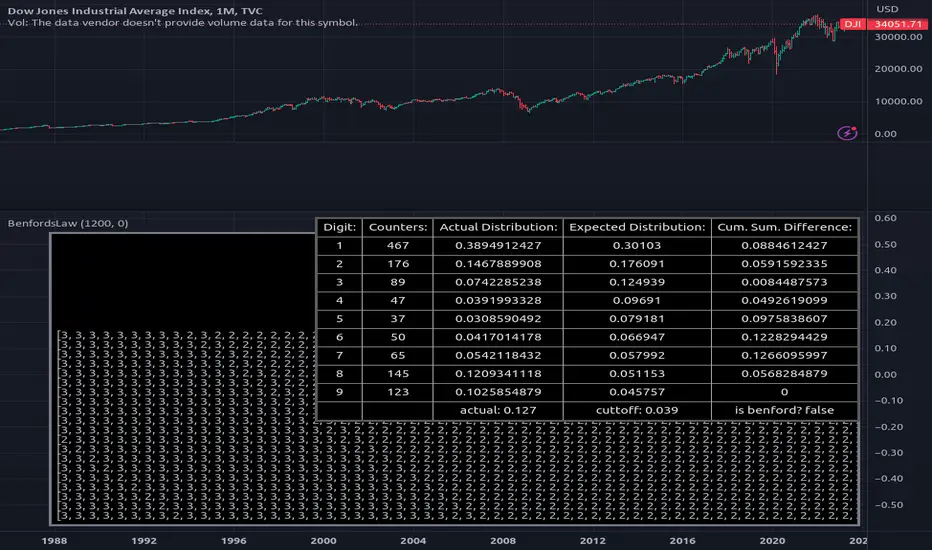
Library "BenfordsLaw"
Methods to deal with Benford's law which states that a distribution of first and higher order digits
of numerical strings has a characteristic pattern.
"Benford's law is an observation about the leading digits of the numbers found in real-world data sets.
Intuitively, one might expect that the leading digits of these numbers would be uniformly distributed so that
each of the digits from 1 to 9 is equally likely to appear. In fact, it is often the case that 1 occurs more
frequently than 2, 2 more frequently than 3, and so on. This observation is a simplified version of Benford's law.
More precisely, the law gives a prediction of the frequency of leading digits using base-10 logarithms that
predicts specific frequencies which decrease as the digits increase from 1 to 9." ~(2)
---
reference:
- 1: en.wikipedia.org/wiki/Benford's_law
- 2: brilliant.org/wiki/benfords-law/
- 4: github.com/vineettanna/Benfords-Law/tree/master
cumsum_difference(a, b)
Calculate the cumulative sum difference of two arrays of same size.
Parameters:
a (float[]): `array<float>` List of values.
b (float[]): `array<float>` List of values.
Returns: List with CumSum Difference between arrays.
fractional_int(number)
Transform a floating number including its fractional part to integer form ex:. `1.2345 -> 12345`.
Parameters:
number (float): `float` The number to transform.
Returns: Transformed number.
split_to_digits(number, reverse)
Transforms a integer number into a list of its digits.
Parameters:
number (int): `int` Number to transform.
reverse (bool): `bool` `default=true`, Reverse the order of the digits, if true, last will be first.
Returns: Transformed number digits list.
digit_in(number, digit)
Digit at index.
Parameters:
number (int): `int` Number to parse.
digit (int): `int` `default=0`, Index of digit.
Returns: Digit found at the index.
digits_from(data, dindex)
Process a list of `int` values and get the list of digits.
Parameters:
data (int[]): `array<int>` List of numbers.
dindex (int): `int` `default=0`, Index of digit.
Returns: List of digits at the index.
digit_counters(digits)
Score digits.
Parameters:
digits (int[]): `array<int>` List of digits.
Returns: List of counters per digit (1-9).
digit_distribution(counters)
Calculates the frequency distribution based on counters provided.
Parameters:
counters (int[]): `array<int>` List of counters, must have size(9).
Returns: Distribution of the frequency of the digits.
digit_p(digit)
Expected probability for digit according to Benford.
Parameters:
digit (int): `int` Digit number reference in range `1 -> 9`.
Returns: Probability of digit according to Benford's law.
benfords_distribution()
Calculated Expected distribution per digit according to Benford's Law.
Returns: List with the expected distribution.
benfords_distribution_aprox()
Aproximate Expected distribution per digit according to Benford's Law.
Returns: List with the expected distribution.
test_benfords(digits, calculate_benfords)
Tests Benford's Law on provided list of digits.
Parameters:
digits (int[]): `array<int>` List of digits.
calculate_benfords (bool)
Returns: Tuple with:
- Counters: Score of each digit.
- Sample distribution: Frequency for each digit.
- Expected distribution: Expected frequency according to Benford's.
- Cumulative Sum of difference:
to_table(digits, _text_color, _border_color, _frame_color)
Parameters:
digits (int[])
_text_color (color)
_border_color (color)
_frame_color (color)
Methods to deal with Benford's law which states that a distribution of first and higher order digits
of numerical strings has a characteristic pattern.
"Benford's law is an observation about the leading digits of the numbers found in real-world data sets.
Intuitively, one might expect that the leading digits of these numbers would be uniformly distributed so that
each of the digits from 1 to 9 is equally likely to appear. In fact, it is often the case that 1 occurs more
frequently than 2, 2 more frequently than 3, and so on. This observation is a simplified version of Benford's law.
More precisely, the law gives a prediction of the frequency of leading digits using base-10 logarithms that
predicts specific frequencies which decrease as the digits increase from 1 to 9." ~(2)
---
reference:
- 1: en.wikipedia.org/wiki/Benford's_law
- 2: brilliant.org/wiki/benfords-law/
- 4: github.com/vineettanna/Benfords-Law/tree/master
cumsum_difference(a, b)
Calculate the cumulative sum difference of two arrays of same size.
Parameters:
a (float[]): `array<float>` List of values.
b (float[]): `array<float>` List of values.
Returns: List with CumSum Difference between arrays.
fractional_int(number)
Transform a floating number including its fractional part to integer form ex:. `1.2345 -> 12345`.
Parameters:
number (float): `float` The number to transform.
Returns: Transformed number.
split_to_digits(number, reverse)
Transforms a integer number into a list of its digits.
Parameters:
number (int): `int` Number to transform.
reverse (bool): `bool` `default=true`, Reverse the order of the digits, if true, last will be first.
Returns: Transformed number digits list.
digit_in(number, digit)
Digit at index.
Parameters:
number (int): `int` Number to parse.
digit (int): `int` `default=0`, Index of digit.
Returns: Digit found at the index.
digits_from(data, dindex)
Process a list of `int` values and get the list of digits.
Parameters:
data (int[]): `array<int>` List of numbers.
dindex (int): `int` `default=0`, Index of digit.
Returns: List of digits at the index.
digit_counters(digits)
Score digits.
Parameters:
digits (int[]): `array<int>` List of digits.
Returns: List of counters per digit (1-9).
digit_distribution(counters)
Calculates the frequency distribution based on counters provided.
Parameters:
counters (int[]): `array<int>` List of counters, must have size(9).
Returns: Distribution of the frequency of the digits.
digit_p(digit)
Expected probability for digit according to Benford.
Parameters:
digit (int): `int` Digit number reference in range `1 -> 9`.
Returns: Probability of digit according to Benford's law.
benfords_distribution()
Calculated Expected distribution per digit according to Benford's Law.
Returns: List with the expected distribution.
benfords_distribution_aprox()
Aproximate Expected distribution per digit according to Benford's Law.
Returns: List with the expected distribution.
test_benfords(digits, calculate_benfords)
Tests Benford's Law on provided list of digits.
Parameters:
digits (int[]): `array<int>` List of digits.
calculate_benfords (bool)
Returns: Tuple with:
- Counters: Score of each digit.
- Sample distribution: Frequency for each digit.
- Expected distribution: Expected frequency according to Benford's.
- Cumulative Sum of difference:
to_table(digits, _text_color, _border_color, _frame_color)
Parameters:
digits (int[])
_text_color (color)
_border_color (color)
_frame_color (color)
Release Notes
v2 minor update.Release Notes
Fix logger version.Pine library
In true TradingView spirit, the author has published this Pine code as an open-source library so that other Pine programmers from our community can reuse it. Cheers to the author! You may use this library privately or in other open-source publications, but reuse of this code in a publication is governed by House rules.
Disclaimer
The information and publications are not meant to be, and do not constitute, financial, investment, trading, or other types of advice or recommendations supplied or endorsed by TradingView. Read more in the Terms of Use.