PROTECTED SOURCE SCRIPT
EMA-Deviation-Corrected N-Pole Gaussian Filter [Loxx]
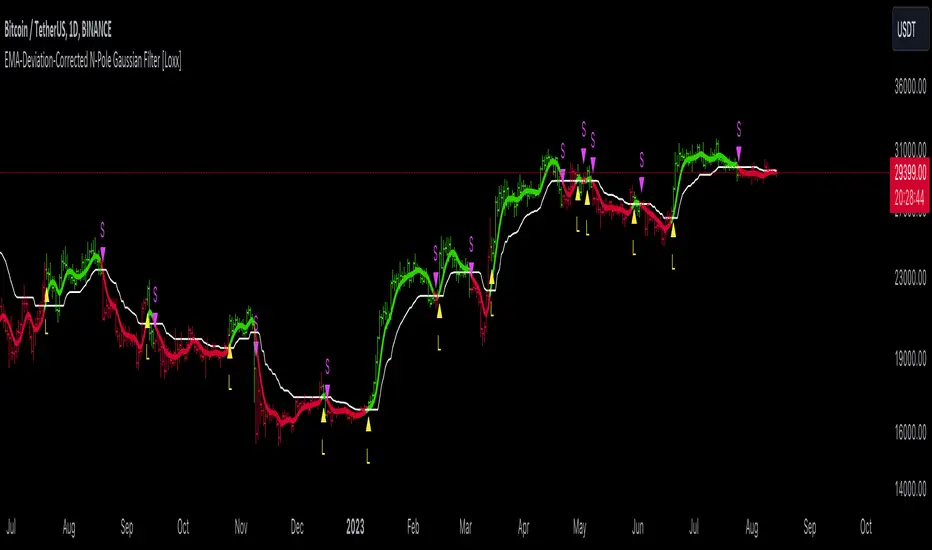
EMA-Deviation-Corrected N-Pole Gaussian Filter is a moving average that uses EMA-deviation correcting to produce signals.
█ EMA-Deviation Correction
The origin of the correcting algorithm can be attributed to Dr. Alexander Uhl, who developed a method to filter the moving average and identify signals. Originally, this method utilized standard deviation as a measure to correct the average values.
However, the current indicator in question employs a modified version of the correcting method. Instead of using standard deviation for calculation, it uses EMA deviation, which stands for Exponential Moving Average deviation. The idea behind using EMA deviation is two-fold:
Efficiency: EMA deviation can be calculated faster than standard deviation, resulting in more efficient code execution.
Signal Reduction: Surprisingly, this modified "correcting" approach generates fewer signals compared to using standard deviation. This is because EMA deviation is more responsive to price changes, making the correcting process less sensitive to whipsaws or false signals.
█ N-Pole Gaussian Filter
N-Pole Gaussian Filter is an advanced Gaussian filter, extending beyond the traditional 4-pole limitation found in Ehlers' original Gaussian Filter formulas. This enhanced version can handle up to 15 poles, but due to precision constraints, going beyond this doesn't yield significantly different results.
A gaussian filter with...
For an equivalent number of poles the lag of a Gaussian is about half the lag of a Butterworth filters: Lag = N*P / pi^2, where,
N is the number of poles, and
P is the critical period
Ehlers Gaussian filter, a creation of John F. Ehlers, is renowned for its smoothing capabilities. It's adept at sidelining rapid price fluctuations more effectively than the standard Exponential Moving Average (EMA), and it does so with minimal lag. The filter's behavior is akin to the Gaussian bell curve, and its mathematical representation varies based on the number of poles it's designed to handle.
In comparison to other filters like the Butterworth, the Gaussian filter boasts about half the lag for a similar number of poles. This is quantified using a specific formula that considers the number of poles and the critical period. The filter's design ensures it operates efficiently, even with minimal data.
█ Included
█ EMA-Deviation Correction
The origin of the correcting algorithm can be attributed to Dr. Alexander Uhl, who developed a method to filter the moving average and identify signals. Originally, this method utilized standard deviation as a measure to correct the average values.
However, the current indicator in question employs a modified version of the correcting method. Instead of using standard deviation for calculation, it uses EMA deviation, which stands for Exponential Moving Average deviation. The idea behind using EMA deviation is two-fold:
Efficiency: EMA deviation can be calculated faster than standard deviation, resulting in more efficient code execution.
Signal Reduction: Surprisingly, this modified "correcting" approach generates fewer signals compared to using standard deviation. This is because EMA deviation is more responsive to price changes, making the correcting process less sensitive to whipsaws or false signals.
█ N-Pole Gaussian Filter
N-Pole Gaussian Filter is an advanced Gaussian filter, extending beyond the traditional 4-pole limitation found in Ehlers' original Gaussian Filter formulas. This enhanced version can handle up to 15 poles, but due to precision constraints, going beyond this doesn't yield significantly different results.
A gaussian filter with...
- One Pole: f = alpha*g + (1-alpha)f
- Two Poles: f = alpha*2g + 2(1-alpha)f - (1-alpha)2f
- Three Poles: f = alpha*3g + 3(1-alpha)f - 3(1-alpha)2f + (1-alpha)3f
- Four Poles: f = alpha*4g + 4(1-alpha)f - 6(1-alpha)2f + 4(1-alpha)3f - (1-alpha)4f
- and so on...
For an equivalent number of poles the lag of a Gaussian is about half the lag of a Butterworth filters: Lag = N*P / pi^2, where,
N is the number of poles, and
P is the critical period
Ehlers Gaussian filter, a creation of John F. Ehlers, is renowned for its smoothing capabilities. It's adept at sidelining rapid price fluctuations more effectively than the standard Exponential Moving Average (EMA), and it does so with minimal lag. The filter's behavior is akin to the Gaussian bell curve, and its mathematical representation varies based on the number of poles it's designed to handle.
In comparison to other filters like the Butterworth, the Gaussian filter boasts about half the lag for a similar number of poles. This is quantified using a specific formula that considers the number of poles and the critical period. The filter's design ensures it operates efficiently, even with minimal data.
█ Included
- Loxx's Expanded Source Types
- Signals
- Alerts
- Bar coloring
Public Telegram Group, t.me/algxtrading_public
VIP Membership Info: patreon.com/algxtrading/membership
VIP Membership Info: patreon.com/algxtrading/membership
Disclaimer
The information and publications are not meant to be, and do not constitute, financial, investment, trading, or other types of advice or recommendations supplied or endorsed by TradingView. Read more in the Terms of Use.