Delta option greek

Delta shows how much the value of a portfolio (strategy) will theoretically change with a change of underlying asset price by 1 point. 

Consider a call option on the S&P 500 futures with a strike price of 4630. Let's say the call price is 54.25 points. Let's say the delta for this option is 0.5. This means that if the price of the S&P 500 futures changes by 1 point, the option price will change by 0.5 and become 54.75. The moneyness of the option influences delta values. In-the-money call options, where the strike price is significantly below the current price of the underlying asset, generally have delta values closer to 1, indicating a stronger correlation between the option price and the underlying asset price. (see below)

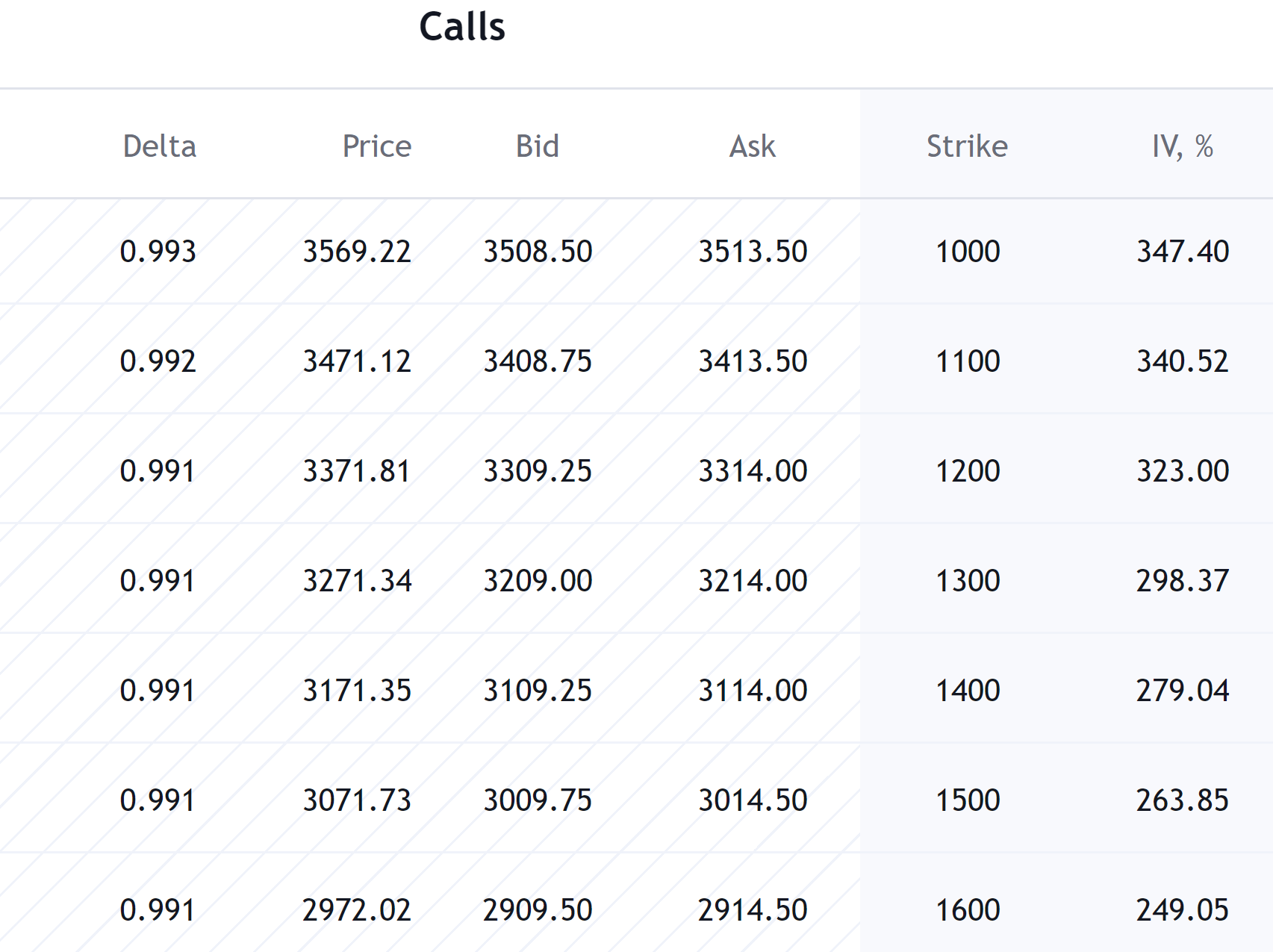
On the other hand, out-of-the-money call options, where the strike price is above the current price of the underlying asset, typically have delta values closer to 0. (see below)

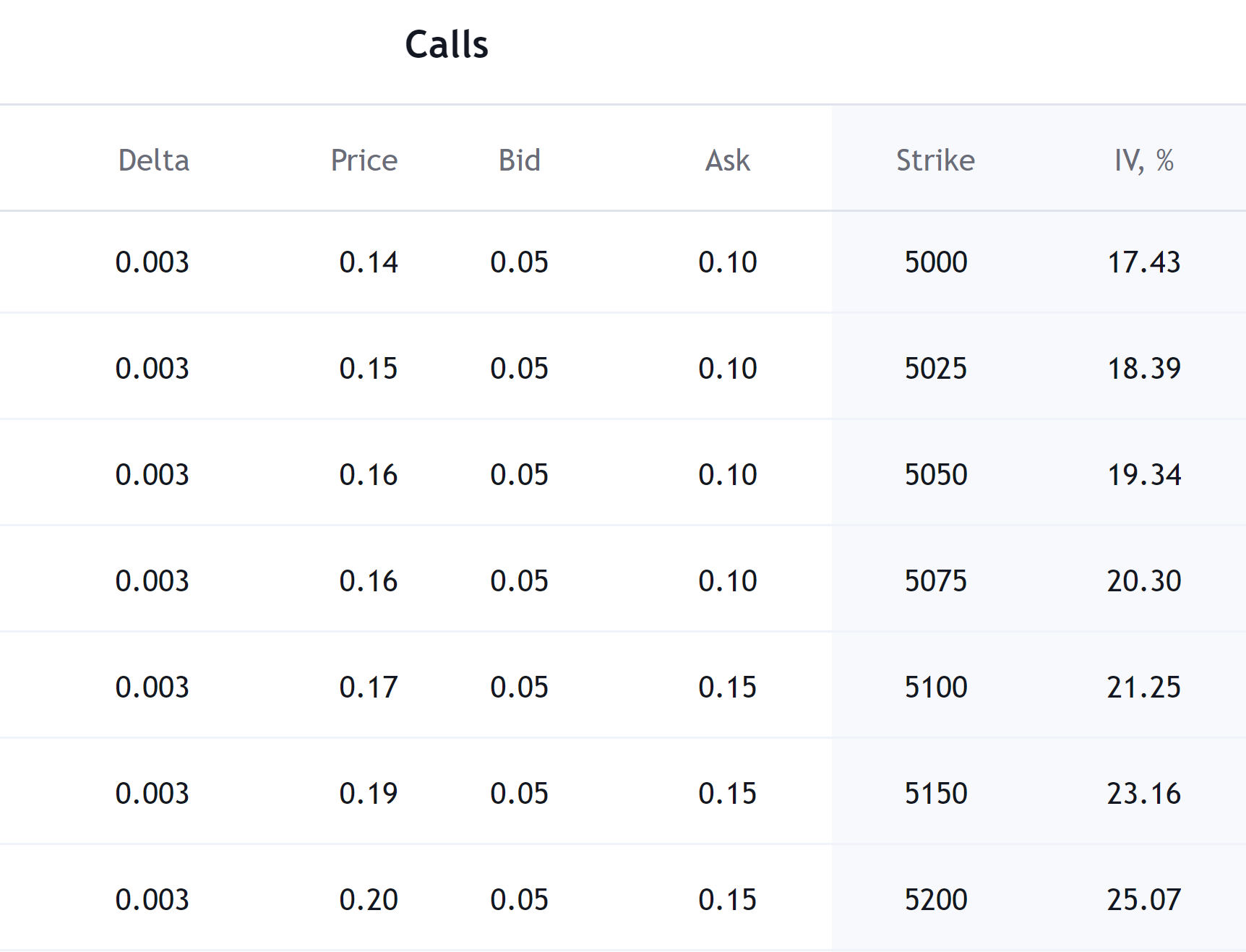
Unlike call options, the relationship between moneyness and delta for put options is inverted. In-the-money put options generally have delta values closer to -1. Out-of-the-money put options typically have delta values closer to 0. At-the-money put options have delta values closer to -0.5.

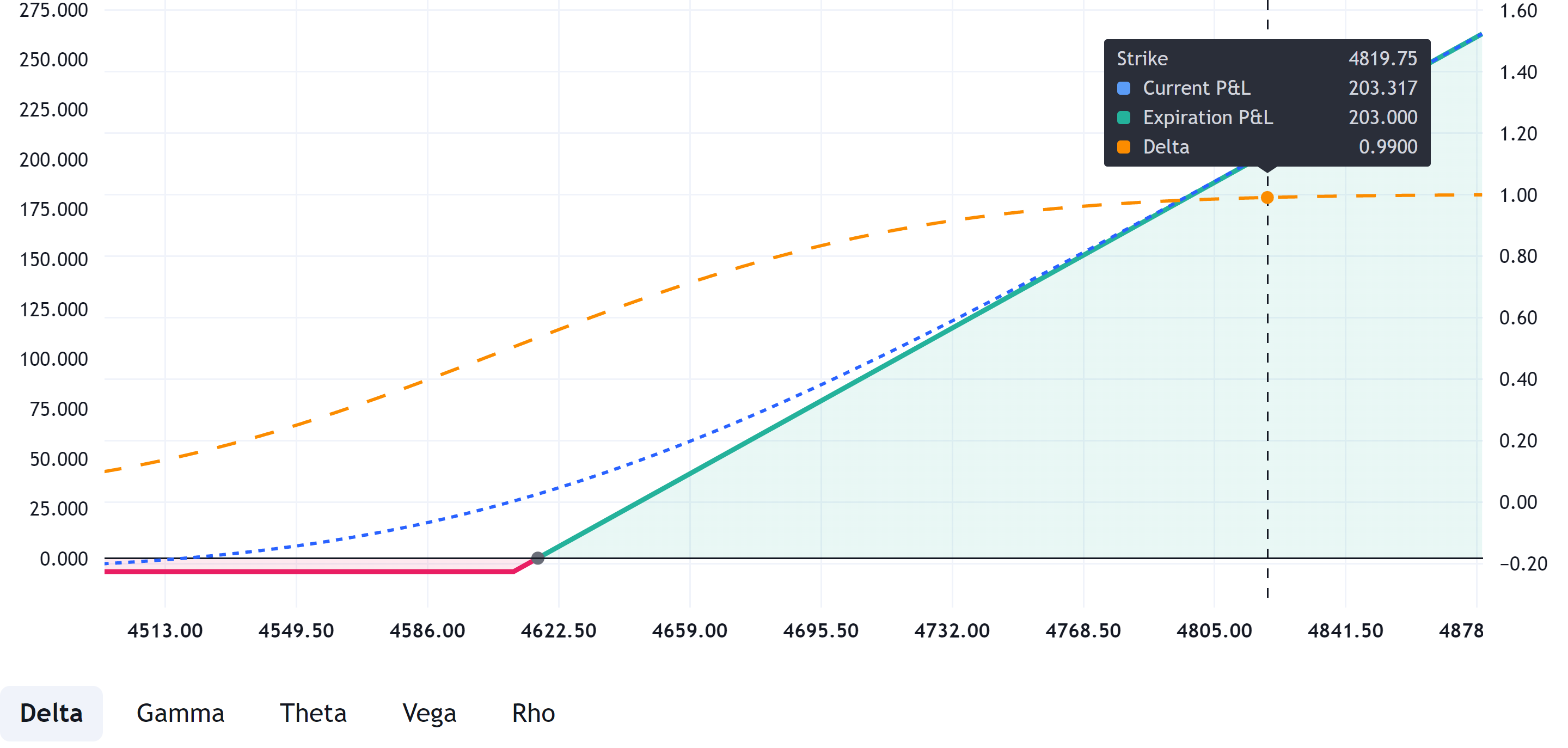
When the price of the underlying asset changes, the option delta also changes. For example, let's again take a call option on the S&P 500 futures with a strike of 4600. Let's assume that the current price of the underlying asset is 4610. If the price of the futures on the S&P 500 index increases to 5000, then the delta of our option will approach 1, which will mean that our option is now deep in-the-money and fluctuations in the price of the underlying asset are reflected in the price of the option 1 to 1. (see below)

And vice versa, if the price of the underlying asset falls sharply, for example, to 4000, then the delta of our option will decrease and approach 0, i.e., fluctuations in the price of the underlying asset will not affect the price of the option. (see below)

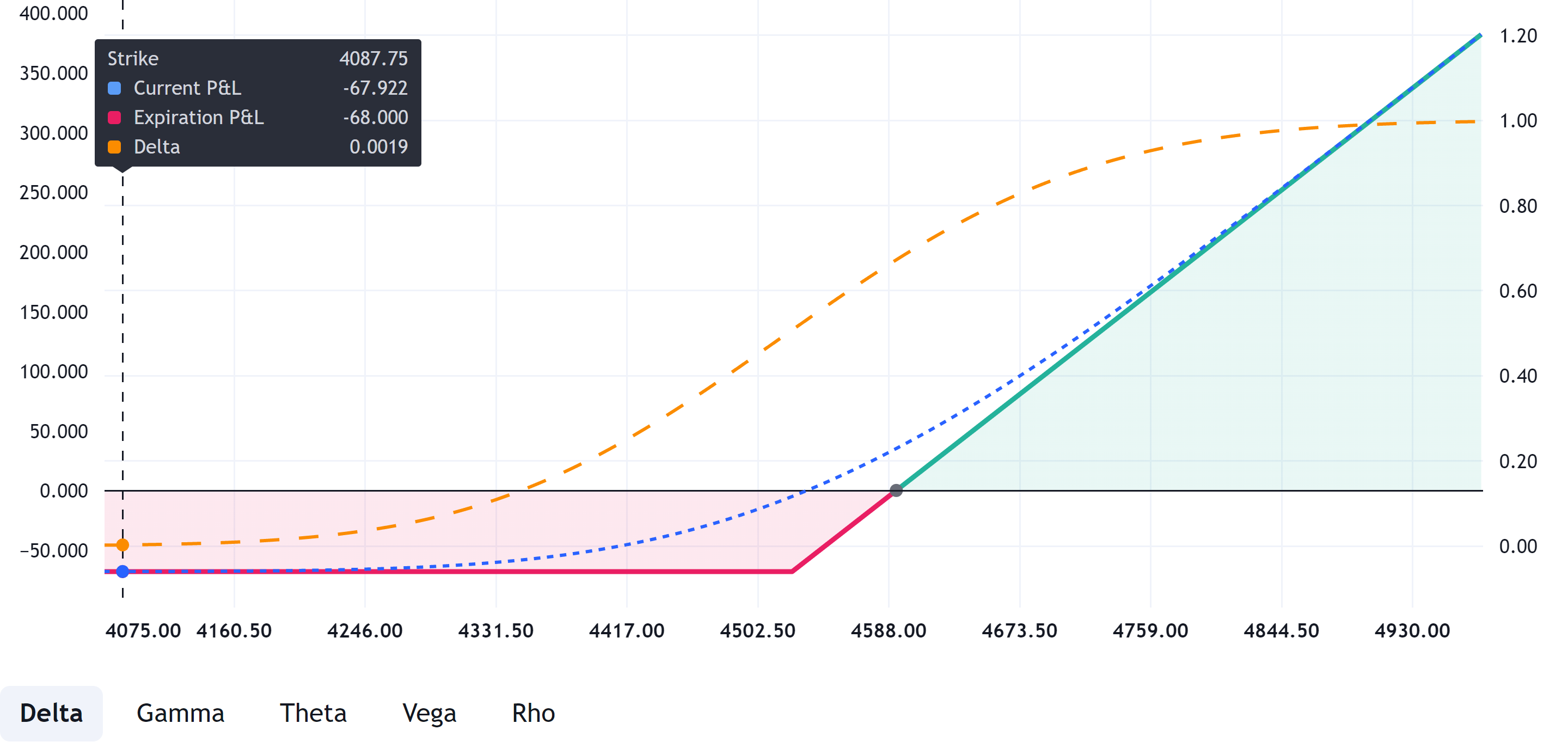
For long put options positions, the delta behaves like a mirror. Its values range from -1 to 0. For put options with strikes much less than the central strike, the delta tends to 0, while for strikes significantly greater than the central strike delta tends to -1.

Delta is used to build delta neutral strategies when a trader expects some significant news and consequently increase or fall of volatility, but cannot predict where the price of the underlying asset will move. An example of such a strategy is Straddle. The one who trades delta neutral strategies wants to take a gain from options price time decay or implied volatility change, while doesn’t want to be affected by underlying price directional change.